3 – Approssimazione caratteristica mediante interpolazione dei dati
Il grafico precedente mostra l’andamento della tensione campionata val(temp). Arduino però per poter restituire la temperatura a cui il termistore è sottoposto, partendo dalla tensione campionata val letta sull’ingresso analogico, richiede l’implementazione della funzione inversa temp(val), il cui grafico è ottenuto invertendo gli assi.
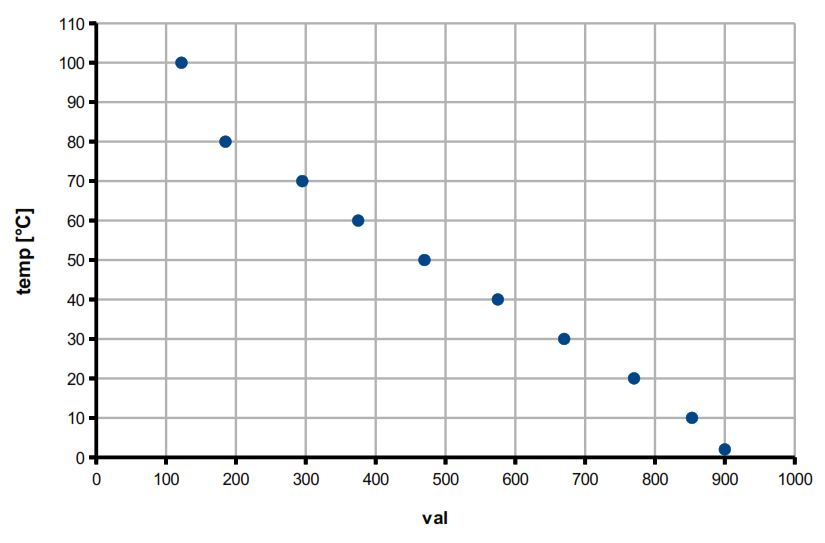
In realtà però i dati raccolti determinano una successione di punti (val_k,temp_k) e non una funzione vera e propria, è quindi necessario far capire ad Arduino quale temperatura è associata ad un valore letto che non è riportato in tabella (cioè tutti quegli infiniti valori compresi tra un punto e l’altro). Per fare ciò si ricorre ad una tecnica chiamata “interpolazione”, che consiste nel determinare una funzione che meglio approssima il grafico. Tra i vari tipi di interpolazione esistenti (polinomiale, trigonometrica, etc), quello adatto a questo scopo è chiamato “interpolazione lineare”.
In sintesi, dati n+1 punti di un grafico, si determinano n rette, ciascuna valida nel rispettivo intervallo tra un nodo di interpolazione e l’altro, ottenendo complessivamente una funzione costituita da un insieme di segmenti che congiungono ciascun punto al successivo.
Prendendo i generici punti P_{k-1} = (x_{k-1}, y_{k-1}) e P_k = (x_k, y_k), se il valore indipendente in ingresso x è compreso tra x_{k-1} e x_k, allora la funzione definita in tale intervallo è una retta y = m_k*x + q_k, dove:
\displaystyle m_k = \frac{y_k-y_{k-1}}{x_k-x_{k-1}} è il coefficiente angolare
q_k = y_k - m_k*x_k è il termine noto
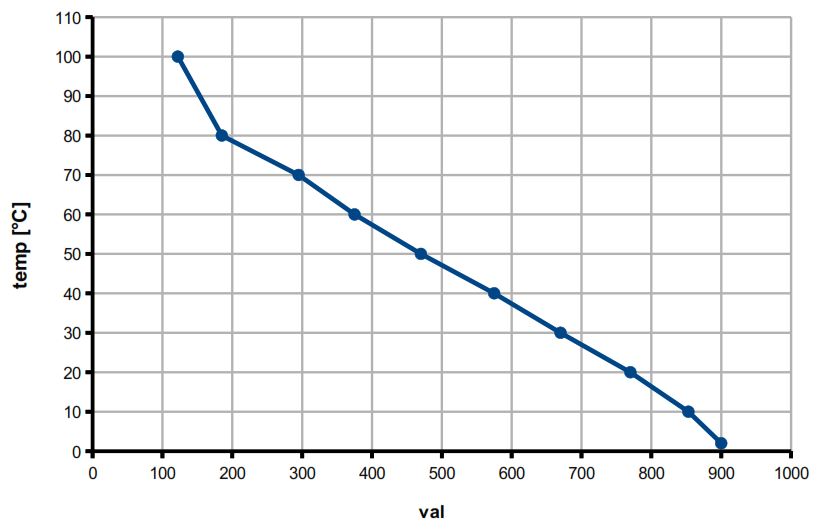
L’algoritmo che verrà impiegato successivamente fa si che la funzione esista anche al di fuori dell’intervallo dei punti dati (estrapolazione), e corrisponde ad un prolungamento dei segmenti estremi. Ovviamente più ci si allontana dall’intervallo dei punti e meno precisa sarà l’approssimazione del fenomeno che si sta analizzando.
17,351 total views, 1 views today
